【応用情報技術者試験】データ構造とアルゴリズムを学ぼう！ ~第4章~整列

アルゴリズムは問題を解決するための手順や方法論（料理のレシピ）、データ構造はデータを効率的に整理・格納する形式（食材の保管方法）を指し、これらはプログラミングの基礎であり、適切な組み合わせでプログラムの性能（速度や効率）を大幅に向上させるために不可欠です。データ構造（配列、リスト、木など）は「何を（データ）」、アルゴリズム（探索、ソートなど）は「どうする（手順）」を決め、両者は密接に連携し、効率的なソフトウェア開発と問題解決の鍵となります。

画像参照：https://mo-gu-mo-gu.com/about-datastructure-algorithm/

整列アルゴリズム

整列アルゴリズム

データ（数値や文字列など）を特定のルール（大小関係や五十音順など）に従って並べ替える（整列させる）ための手順や手法の総称です。プログラミングにおいて、データベース検索や商品表示などでデータを効率的に整理するために不可欠な技術で、バブルソート、クイックソート、マージソートなど様々な種類があり、それぞれ処理速度や効率が異なります。

アルゴリズム	手順の概要	時間計算量
バブルソート	隣接する要素同士を比較し、順序が逆なら交換することを繰り返してデータを並べ替えします。	O(n²)
選択ソート	データ列の中から最小（または最大）の要素を繰り返し見つけ出し、それを正しい位置（未整列部分の先頭）に移動（交換）していくことで全体を整列させます。	O(n²)
挿入ソート	データを「整列済み」と「未整列」の2つに分け、未整列の要素を1つずつ取り出して整列させます。	O(n²)
クイックソート	データを基準値で「小さいグループ」と「大きいグループ」に分割し、その分割操作を再帰的に繰り返すことで高速に整列させます。	O(nlogn)
マージソート	データを要素が1つになるまで繰り返し2分割し、その後、「マージ」して整列済みのリストを統合していきます。	O(nlogn)
シェルソート	離れた位置にある要素同士を先にソートし、徐々に間隔を狭めながらソートを繰り返す手法です。	O(n^1.25)
ヒープソート	ヒープと呼ばれる特殊な二分木構造（木構造）を利用してデータを効率的に並べ替えます。	O(nlogn)

バブルソート

バブルソートは、

隣接する要素同士を比較し、順序が逆なら交換することを繰り返してデータを並べ替える（ソートする）最も基本的なアルゴリズムの一つです。水中の泡が浮き上がるように、大きな値（または小さな値）が端に移動していく様子に由来し、「隣接交換法」とも呼ばれます。実装は容易ですが、データ量が増えると非常に遅くなる（計算量がO(n²)）ため、実用よりも学習用として用いられます。

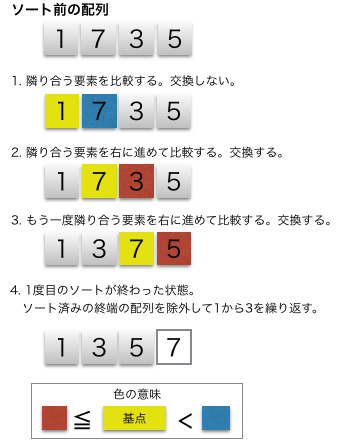
画像参照：https://www.codereading.com/algo_and_ds/algo/bubble_sort.html

仕組み

隣接比較と交換: リストの先頭から隣り合う2つの要素を比較し、もし順序が間違っていれば（例：昇順で左が大きい）、それらを入れ替えます。
一周の処理: リストの最後までこの比較・交換を繰り返します。この1回の繰り返しで、最も大きな（または小さな）要素がリストの端（右端）に移動します。
繰り返す: 最も端に移動した要素は除外し、残りの未整列部分で同様の処理を繰り返します。これをリストの長さが1になるまで続けます。
終了条件: 交換が発生しなくなったら、ソートは完了です。

特徴

長所:
- アルゴリズムが単純で理解しやすく、実装も容易です。
- データ領域をあまり必要としない「インプレースソート」であり、同じ値の順序が変わらない「安定ソート」です。
短所:
- 最悪・平均計算量がO(n²)と遅く、大量のデータには向きません。

具体例（昇順）

[5, 1, 4, 2, 8]

1周目:
- (5, 1) → 交換:
- (5, 4) → 交換:
- (5, 2) → 交換:
- (5, 8) → 交換なし:
- 結果: 最大値の8が右端に移動。
2周目:
- (1, 4) → 交換なし:
- (4, 2) → 交換:
- (4, 5) → 交換なし:
- 結果: 2番目に大きい値の5が右から2番目に移動。
3周目:
- (1, 2) → 交換なし:
- (2, 4) → 交換なし:
- 結果: 3番目に大きい値の4が右から3番目に移動。
4周目:
- (1, 2) → 交換なし:
- 結果: 4番目に大きい値の2が右から4番目に移動。
最終結果: [1, 2, 4, 5, 8]。

選択ソート

選択ソートとは、データ列の中から最小（または最大）の要素を繰り返し見つけ出し、それを正しい位置（未整列部分の先頭）に移動（交換）していくことで全体を整列させる、最も基本的なソート（並び替え）アルゴリズムです。未整列部分の最小値を探し、未整列部分の先頭要素と入れ替える操作を繰り返すため、処理がシンプルで実装しやすい反面、計算量（時間効率）はO(n²)と遅い部類に入りますが、安定した処理時間で予測しやすい特徴があります。

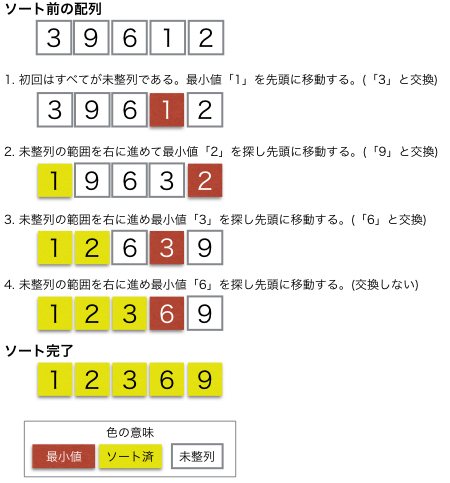
画像参照：https://www.codereading.com/algo_and_ds/algo/selection_sort.html

仕組み

配列を「整列済み」と「未整列」に分ける: 最初は全体が「未整列」です。
最小値の探索: 未整列の部分（最初は配列全体）から最も小さい値を探します。
交換（入れ替え）: 見つけた最小値を、未整列部分の先頭の要素と交換します。
範囲の更新: 先頭の要素が整列済みになるので、未整列部分を一つ後ろにずらします。
繰り返し: 未整列部分がなくなるまで、2〜4の操作を繰り返します。

特徴

実装が容易: アルゴリズムがシンプルで、教育目的や短いデータ列のソートに適しています。
計算量: O( $n squared$ )。データ量が増えると処理時間が大幅に増加します。
インプレースソート: 追加のメモリ領域をほとんど必要としません。
不安定ソート: 同じ値の要素の相対的な順序は保証されません（ただし、少し変更すれば安定ソートにできる場合もあります）。

挿入ソート

挿入ソートとは、データを「整列済み」と「未整列」の2つに分け、未整列の要素を1つずつ取り出して整列済みの適切な位置に挿入していく、シンプルで直感的な並べ替え（ソート）アルゴリズムです。トランプを手札に並べるように、新しいカード（データ）を既にある並びの正しい場所に差し込むイメージで、小規模データや教育用途、ほぼ整列済みのデータで効率が良いのが特徴です。

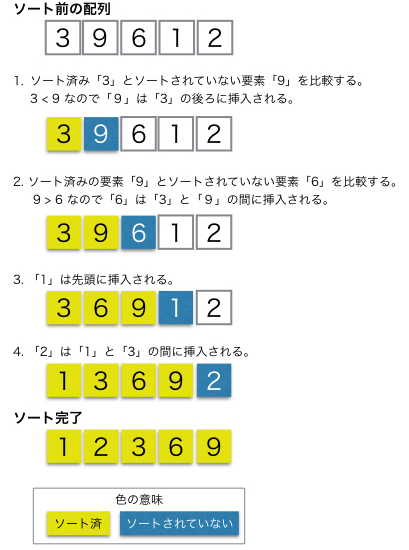
画像参照：https://www.codereading.com/algo_and_ds/algo/insertion_sort.html

仕組み

開始: 最初の1つ（または2つ）のデータを「整列済み」とみなします。
要素の取り出し: 未整列のデータ列から次の要素を1つ取り出します。
位置の探索と挿入: 取り出した要素を、整列済みの部分の先頭から比較し、大小関係が正しい位置（適切な場所）に挿入します。挿入のために、それ以降の要素は後ろにずらします。
繰り返し: 未整列のデータがなくなるまで2, 3の操作を繰り返すと、すべてのデータが整列されます。

特徴

シンプル: 実装が容易で、アルゴリズムの理解がしやすい。
適用: 手札のトランプを並べ替える動作に似ているため、直感的。
効率:
- 最良（ほぼ整列済み）: 非常に高速（O(n)）。
- 最悪（逆順）: O(n²)となり、大規模データでは非効率。
応用: 挿入ソートを高速化したものとしてシェルソートがあります。

まとめ

挿入ソートは、「少しずつ正しい場所に差し込んでいく」という基本動作でデータを並べ替える方法で、そのシンプルさから多くのソートアルゴリズムの基礎として利用されます。

クイックソート

クイックソートは、データを基準値（ピボット）で「小さいグループ」と「大きいグループ」に分割し、その分割操作を再帰的に繰り返すことで高速に整列（ソート）する分割統治法に基づくアルゴリズムです。平均的には非常に高速ですが、最悪ケースでは処理が遅くなる欠点もあり、安定ソート（同値要素の相対順序を保持）ではない点が特徴です。

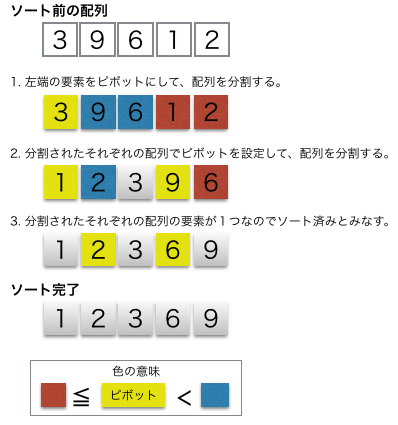
画像参照：https://www.codereading.com/algo_and_ds/algo/quick_sort.html

仕組み

基準値（ピボット）の選択: 整列したい範囲から一つの要素を基準値として選びます。先頭、末尾、中央、ランダムな値などが使われますが、選び方で効率が変わります。
分割（パーティション）: 基準値より小さい要素は左側へ、大きい要素は右側へ移動させ、基準値を真ん中に配置します。この操作で、基準値の位置は確定します。
再帰: 分割された「小さいグループ」と「大きいグループ」それぞれに対して、ステップ1と2の操作を繰り返します。
終了: グループ内の要素が1つ（または0個）になったら、分割を終了します。すべてのグループで終了すると、全体がソートされます。

特徴

高速性: 平均計算量が O(nlogn)と非常に高速で、実用上よく使われます。
最悪計算量: 基準値の選び方が悪いと O(n²) になり、遅くなることがあります（例: 常に最小値が選ばれる場合）。
安定性: 不安定ソートであり、同じ値の要素の元の順序は保証されません。
メモリ: 外部記憶領域をあまり必要としない「インプレースソート」ですが、再帰呼び出しのためにスタック領域O(logn）は必要です。

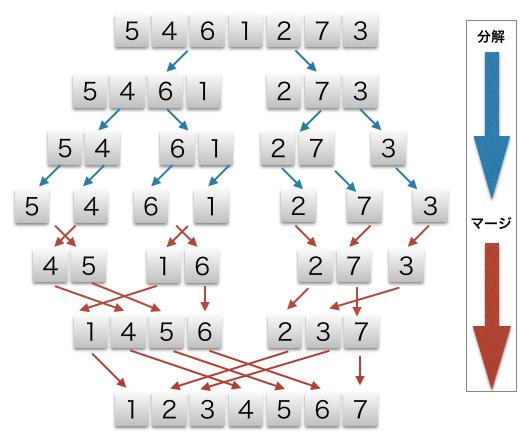
マージソート

マージソートは、「分割統治法」を用いた効率的なソート（並べ替え）アルゴリズムで、データを要素が1つになるまで繰り返し2分割し、その後、「マージ（結合）」して整列済みのリストを統合していく方法です。特徴は、安定ソートであることと、最悪ケースでも計算量がO(nlogn)と高速な点ですが、追加のメモリ領域が必要になる点に注意が必要です。

画像参照：https://www.codereading.com/algo_and_ds/algo/merge_sort.html

特徴

安定性:同じ値の要素の元の順序が保たれる「安定ソート」です。
計算量: O(logn)で、データ量が増えても効率的です。
メモリ:追加の作業領域（元の配列と同じくらいのサイズ）が必要になるのが主な欠点です。
用途:大規模データや、安定性が求められる場面で有効です。

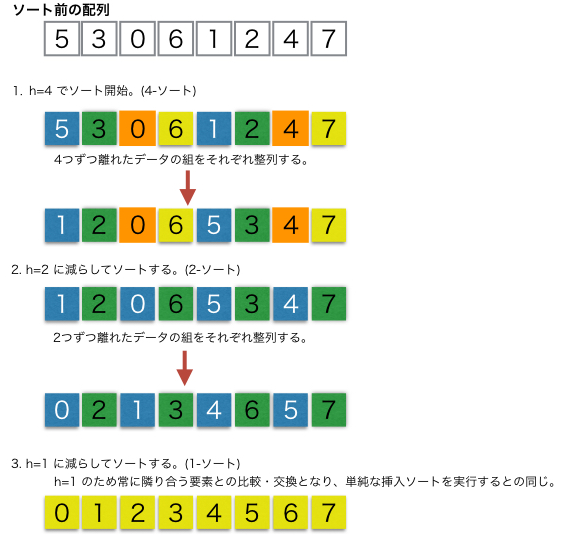
シェルソート

シェルソートとは、挿入ソートを改良した効率的な整列（ソート）アルゴリズムで、離れた位置にある要素同士を先にソートし、徐々に間隔を狭めながらソートを繰り返す手法です。これにより、バラバラなデータでも段階的に「ざっくり」と並べ替え、最終的に「細かい」部分を整えることで、単純な挿入ソートよりも高速に動作させることができます。

画像参照：https://www.codereading.com/algo_and_ds/algo/shell_sort.html

仕組み

間隔（ギャップ）の設定: まず、データ全体に対して、ある程度離れた位置（例: $cap N / 2$ 、 $cap N / 4$ …）の要素だけを抽出した部分列を作ります。
部分列での挿入ソート: その部分列に対して挿入ソートを行います。
間隔の縮小と繰り返し: 間隔を徐々に小さく（例: $cap N / 2 right arrow cap N / 4 right arrow … right arrow 1$ ）しながら、ステップ1と2を繰り返します。
最終ステップ: 最終的に間隔が1になると、これは通常の挿入ソートと同じ状態になりますが、この時点ではデータがかなり整っているため、高速に処理が完了します。

特徴

高速性: 挿入ソートが「ほとんどソート済み」のデータに強い性質を活かし、大規模データでも比較的高速に動作します。
実装の容易さ: 比較的シンプルで実装しやすいアルゴリズムです。
不安定ソート: 挿入ソートとは異なり、同じ値の要素の相対的な順序が保証されない「不安定ソート」です。

例え話
「引っ越しの荷造り」に似ています。

まず部屋ごとにざっくり不要なものを捨て（大まかな整理）。
次に箱ごとに整理し（徐々に間隔を狭める）。
最後に段ボールの中を丁寧に整える（間隔1での挿入ソート）。

この「段階的な整理」が、シェルソートの効率性の鍵です。

ヒープソート

ヒープソートとは、ヒープと呼ばれる特殊な二分木構造（木構造）を利用してデータを効率的に並べ替える（ソートする）アルゴリズムです。配列データを「親ノードが子ノードより常に大きい（または小さい）」というヒープの性質を満たす木構造に変換し、最大値（または最小値）を先頭から順に取り出す操作を繰り返すことで、最終的にソートされた配列を得ます。

画像参照：https://www.codereading.com/algo_and_ds/algo/heap_sort.html

仕組み

ヒープ構造の作成: 未整列のデータ（配列）を、ヒープの条件（親ノードが子ノードより大きい/小さい）を満たす二分木（最大ヒープまたは最小ヒープ）に変換します。
最大値（最小値）の抽出: ヒープ構造の根（ルート）にある要素が最大値（または最小値）なので、これを配列の末尾に移動させます。
ヒープの再構築: 末尾に移動した要素の代わりに、ヒープの根に移動してきた要素で木構造を「ヒープ化（再構成）」します。
繰り返し: この「抽出と再構築」の作業を、配列の要素がなくなるまで繰り返します。

特徴

計算量: 最良・最悪・平均計算量がすべて O(nlogn)で、比較ソートの中では高速な部類です。
インプレースソート: 追加のメモリ領域をほとんど必要としない（インプレースで実行可能）アルゴリズムです。

「ヒープ」という言葉の注意点
メモリ管理で使われる「ヒープ領域」とは別の概念で、データ構造としての「ヒープ（heap）」を指します。