【応用情報技術者試験】コンピュータ科学基礎理論を学ぼう！ ~第3章~小数値の表現

コンピュータ内部では2進数を用いて小数点を表現します。

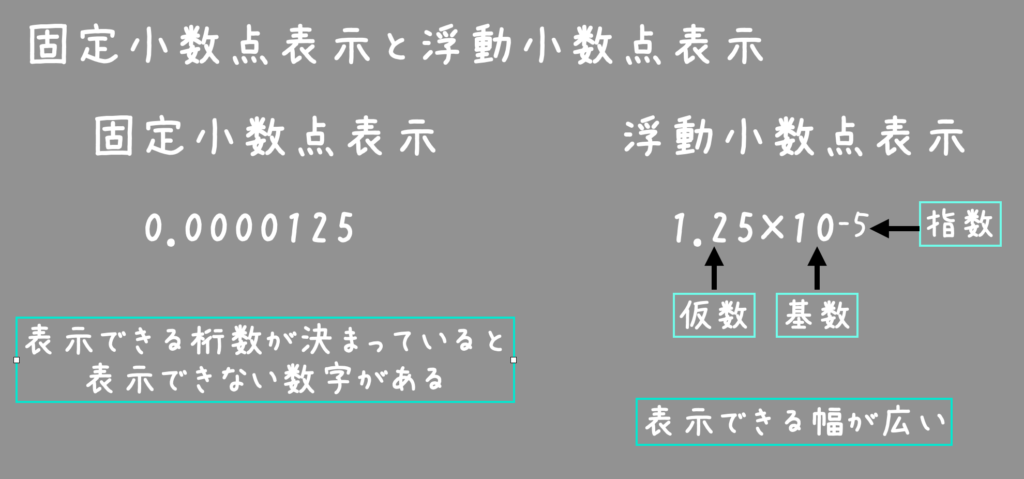
固定小数点数 : 小数点の位置を固定して扱う方式。
浮動小数点数 : 小数点の位置をずらして表現する方式。極端に大きい・小さい数を扱える。
- 構造: 符号部（正負）、指数部、仮数部の3つの情報に分けて管理。
- 規格: IEEE 754 が一般的。単精度（32ビット）や倍精度（64ビット）がある。

画像参照：https://shikaku.pepenoheya.blog/basic_information_ieeeformat/

固定小数点数
浮動小数点数
1. 浮動小数点数の正規化
2. IEEE 754における浮動小数点数

固定小数点数

固定小数点数は、コンピュータが数値を扱う際、あらかじめ決められた位置に小数点を固定して表現する形式です。整数部と小数部の桁数が固定されており、主に整数と同じ回路・計算方式を用いるため、高速かつ情報落ち（精度低下）が起きないという特徴を持ちます。計算速度が重要なDSP（信号処理）や、1円の誤差も許されない金融計算などに適しています。

特徴

小数点の位置が固定: 10進数で言えば、123.45、12.345、1.2345 のように「下から2桁目」など位置が決まっている。
高速計算: 整数演算と全く同じ計算命令を使えるため、ハードウェアやCPUで高速に処理できる。
固定精度: 数値が小さくても大きくても精度が一定。
範囲が狭い: 扱える数の範囲は浮動小数点数に比べて狭い。
情報落ちなし: 巨大な数と小さな数の加減算を行っても、精度が落ちない。

具体的な仕組み（2進数の場合）

16ビットのメモリを例にして、8ビットを整数部、8ビットを小数部として使う場合（8.8形式）:

データ：00000001 10000000（16ビット）
小数点の位置：00000001 . 10000000
値：1 + 0.5 =1.5

システム上は「384」という整数として計算し、プログラム側で結果を1/2⁸倍して1.5と解釈する。

固定小数点数と浮動小数点数の比較

特徴	固定小数点数	浮動小数点数
計算速度	高速	やや遅い
精度	一定 (固定)	範囲に依存 (可変)
数値の範囲	狭い	非常に広い
主な用途	金融・DSP・3DCG	科学計算・グラフィックス

用途

銀行・金融システム: 0.1円以下の誤差が許されない計算（固定小数点数の利用が適している）。
組込みシステム・DSP: 低消費電力、高速性が求められる信号処理。
レトロゲームや3DCG: 浮動小数点ユニットがない古いCPUや、計算速度が最優先される場合。

固定小数点数は「少数」と呼ぶが、小数点の位置を最後に固定すれば整数も同様に扱えます。

浮動小数点数

浮動小数点数は、コンピュータで実数（小数）を扱う際に、符号部・指数部・仮数部の3要素に分けて表現する方式です。小数点の位置を固定せず動的に扱うため、非常に小さな数から大きな数まで、限られたビット数で効率的に表現できます。主に32ビットの単精度64ビットの倍精度があり、IEEE 754 規格が広く使われます。

仕組み

数値を ±(仮数) × (基数)^指数という形式（科学的表記法）で表現する。

符号部 : 正（+）か負（-）か。0なら正、1なら負を表す。
仮数部 : 有効数字の桁並び。
指数部 : 小数点の位置を示す。

例えば、10進数の「-4.375」は2進数で「-1.00011₂ × 2²」と表現でき、符号部に「-」、仮数部に「1.00011」、指数部に「2」が格納される仕組みである。

主な特徴と精度

単精度浮動小数点数 (32bit): 約からまでの範囲、有効桁数は10進数で約6~7桁。
倍精度浮動小数点数 (64bit): 約からまでの範囲、有効桁数は10進数で約15~16桁。
利点: 非常に大きな範囲の数値を表現できる。
欠点: 2進数で表現できない小数が存在するため、計算結果に微小な誤差（誤差）が生じることがある。

浮動小数点数の正規化

浮動小数点の正規化は、数値を1.XXX × 基数^指数の形式（特に2進数では1.XXX × 2ⁿ）に整える処理です。仮数部の最上位桁を0以外（2進数では必ず1）にすることで、有効桁数を最大化し、計算精度を保ち、データ表現を統一します。

正規化の仕組みと重要性

目的: 計算結果の有効桁数を最大にし、丸め誤差を最小限に抑えるため。
方法: 小数点を移動させ、整数部分が1桁（0以外）になるように調整し、その分指数部を増減させる。

IEEE 754における正規化（2進数）
2進数では、1桁目を「1」にすることで、1.000…から1.111…の範囲（実質1以上2未満）に仮数を調整します。

例：101.011₂ × 2² → 1.01011₂ × 2⁴（正規化）

なぜ正規化が必要か
同じ数値を複数の形式で表現できる（例：0.1 × 2¹ = 0.01 × 2²）ことから、コンピュータが演算を効率的かつ正確に行うために、1つの「1.XXX」という形に統一する必要がある。

IEEE 754における浮動小数点数

IEEE 754は、コンピュータで実数（浮動小数点数）を表現・演算する際の国際標準規格です。符号、指数、仮数部を特定のビット数に割り当て、32ビット（単精度）や64ビット（倍精度）で、極めて大きな値から小さな値までを近似的に表します。多くのプログラミング言語（C, Java, Python等）で採用されており、計算結果の互換性を保証します。

IEEE 754の主な特徴と構造

定義: 符号部（1ビット）、指数部、仮数部に分かれており、2進数で実数を表現する方式。
表現の形式: 主に2つの基本形式が存在する。
- 単精度: 32ビット（符号1 + 指数8 + 仮数23）。
- 倍精度 : 64ビット（符号1 + 指数11 + 仮数52）。
特徴: 仮数部の最上位ビットを「1」に固定する（ケチ表現）ことで、実質的な精度を向上させている。
特殊値のサポート: 0、無限大 (♾️、-♾️)、非数（NaN：Not a Number）といった特殊な値を定義。
丸めモード: 最近接偶数への丸め、ゼロ方向への丸め、 +♾️方向への丸め、-♾️方向への丸めを規定。