【応用情報技術者試験】コンピュータ科学基礎理論を学ぼう！ ~第8章~論理演算とシフト演算

コンピュータの演算は、CPU（中央演算装置）が0と1のデジタル信号に基づき、主に「加算」のみで算術計算（+,-,*,/）を行う機能です。減算は補数、乗除算はシフト演算で加算に変換し、論理回路（AND, OR, NOT）を用いて高速に処理します。これはコンピュータの根幹機能であり、文字、画像、音声データもすべてこの高速な数値計算によって処理されています。

画像参照：https://e-words.jp/w/%E3%82%B3%E3%83%B3%E3%83%94%E3%83%A5%E3%83%BC%E3%82%BF.html

論理演算
シフト演算
1. 論理シフト
2. 算術シフト

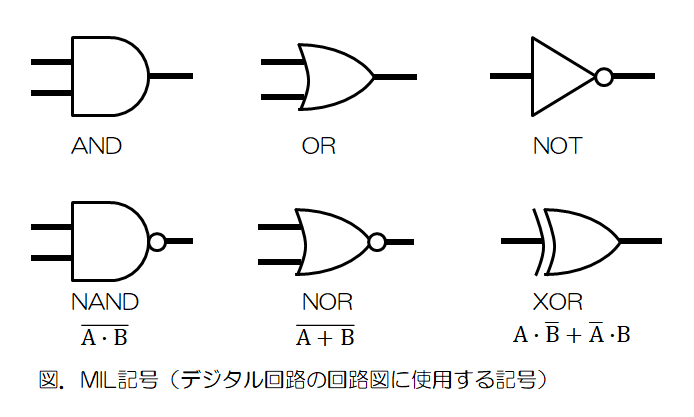
論理演算

論理演算は、真(1)または偽(0)の真理値に基づいて論理回路やビット演算を行う計算です。基本となるのはAND（論理積）、OR（論理和）、NOT（否定）、XOR（排他的論理和）の4種で、これにNAND（否定論理積）、NOR（否定論理和）を加えた6種が重要です。

画像参照：https://basics.k-labo.work/2017/08/31/%E8%AB%96%E7%90%86%E6%BC%94%E7%AE%97/

主要な論理演算

真(1)・偽(0)を用いた演算の定義は以下の通りです。

AND (論理積): 両方が1のときのみ1。
OR (論理和): いずれかが1のときに1。
NOT (否定): 入力を反転する（1→0、0→1）。
XOR (排他的論理和): 一方だけが1のときに1。
NAND (否定論理積): ANDの逆。10以外は1。
NOR (否定論理和): ORの逆。両方0のときのみ1。

論理演算一覧（真理値表）

2つの入力A, Bに対する結果は以下の通りです。

入力A	入力B	NOT A	AND (A·B)	OR (A+B)	XOR	NAND	NOR
0	0	1	0	0	0	1	1
0	1	1	0	1	1	1	0
1	0	0	0	1	1	1	0
1	1	0	1	1	0	0	0

補足

ビット演算: コンピュータではこれらの演算を2進数のビット列（8bitなど）に対して各桁ごとに適用します。
NAND/NORの万能性: NANDゲート（またはNORゲート）の組み合わせだけで、他のすべての論理演算（AND, OR, NOT, XOR）を構成できるため、ハードウェア設計において重要です。

シフト演算

シフト演算は、コンピュータの2進数（ビット列）を左右に移動させる操作です。左へシフトすると2ⁿ倍、右シフトすると1/2ⁿ倍（除算）となり、高速な乗除算として利用されます。符号を無視する「論理シフト」と、符号を保持する「算術シフト」の2種類が存在します。

主な種類と特徴

シフト演算は、コンピュータのハードウェア負荷が少ないため、高速な計算に用いられます。

左シフト (<<): ビット列を左に移動させ、空いた右端に0を補充する。1ビット左へずらすごとに値は2倍になる。
論理右シフト (>>> / >>): ビット列を右に移動させ、空いた左端に0を補充する。
算術右シフト (>>): 最上位ビット（符号ビット）を保持したまま右にシフトする。負の数を2で割る際に使用する。

具体例

1バイト（8ビット）のデータ 00001010 (10進数の10) に対する操作例：

左に1ビットシフト (10 << 1):
- 結果: 00010100 (10進数の20)
- 2倍になる。
右に1ビットシフト (10 >> 1):
- 結果: 00000101 (10進数の5)
- 1/2倍になる。

用途

高速な乗算・除算: の掛け算や割り算。
ビットマスク処理: 特定のビットの抽出や変更。
データ圧縮: データの配置変更。
難読化: セキュリティ対策におけるコードの難読化。

シフト演算は、基本情報技術者試験などのコンピュータ基礎理論において重要で、論理シフトと算術シフトの違い（特に負の数の処理）を理解することがポイントです。

論理シフト

論理シフトは、符号（＋/－）を考慮せず、2進数のビット列全体を左右に移動させる演算です。あふれたビットは捨てられ、空いたビットには常に「0」が埋められます。符号なし整数や、ビット単位の操作に利用されます。

特徴と種類

特徴: 最上位ビット（符号ビット）を特別扱いせず、他のビットと同じように移動します。
論理左シフト:
- ビット列を左にずらす。
- 空いた右端のビットに「0」を入れる。
- ビットずらすごとに値が2倍になる（オーバーフローに注意）。
論理右シフト:
- ビット列を右にずらす。
- 空いた左端のビットに「0」を入れる。
- ビットずらすごとに値が1/2倍になる。

算術シフトとの違い

論理シフト: 符号を無視し、空いたところに「0」を入れる（主に符号なし整数用）。
算術シフト: 符号ビットを保持し、右シフトでは空いた場所に符号ビットを埋める（主に符号付き整数用）。

主な用途
データ圧縮、ビットマスク生成、高速な2のべき乗の乗除算、ビット単位のデータの詰め替えなどに使用されます。

算術シフト

算術シフトは、符号付き整数（2の補数表現）の符号ビット（最上位ビット）を固定したまま、ビット列を左右に移動させる演算。主に2進数の乗算・除算に用いられ、左シフトで2倍（2ⁿ倍）、右シフトで1/2倍（1/2ⁿ倍）の計算を高速に行う。符号（正負）が維持されるのが特徴。

特徴と動作

符号の維持: 最上位ビット（MSB）を固定し、符号ビット以外のビットのみを操作する。
算術左シフト: ビット列を左にずらし、空いた右端に「0」を補充する。符号が変わらない範囲で2倍、4倍、8倍となる。
算術右シフト: ビット列を右にずらし、空いた左端に符号ビット（負数なら1、正数なら0）をコピーして埋める。これにより負数の符号が維持される。
用途: コンピュータのCPUレベルでの高速な乗除算、データ処理。

動作例（8ビット）

操作	2進数表現	10進数表現	動作の解説
元の値	`11111000`	-8	符号ビットは1
1ビット左シフト	`11110000`	-16	2倍 ((-8)×2)。右に0補充。
1ビット右シフト	`11111100`	-4	1/2倍 ((-8)÷2)。左に符号1を補充。

論理シフトとの違い

論理シフト: 符号を無視し、全ビットを一律に移動。右・左シフト共に空いたビットに「0」を詰める。符号なし整数（unsigned）に適用される。
算術シフト: 符号ビットを保護するため、右シフト時に空いたビットへ符号ビットを詰める。

負の数を右へシフトする際、論理シフトでは正の数になってしまうが、算術シフトでは正しく負の数のまま 1/2 倍されるため、符号付きデータの演算に適している。