アルゴリズムは問題を解決するための手順や方法論(料理のレシピ)、データ構造はデータを効率的に整理・格納する形式(食材の保管方法)を指し、これらはプログラミングの基礎であり、適切な組み合わせでプログラムの性能(速度や効率)を大幅に向上させるために不可欠です。データ構造(配列、リスト、木など)は「何を(データ)」、アルゴリズム(探索、ソートなど)は「どうする(手順)」を決め、両者は密接に連携し、効率的なソフトウェア開発と問題解決の鍵となります。

画像参照:https://mo-gu-mo-gu.com/about-datastructure-algorithm/
時間計算量(オーダ)
時間計算量とは、アルゴリズム(手順)が問題を解くのに必要な処理の回数(ステップ数)が、入力データの量(n)が増えるにつれてどれくらい増えるかを示す指標で、{O(n)}(ビッグオー記法)で表し、計算の速さや効率を評価する際に使われます。これは実際の実行時間(秒)ではなく、入力サイズnに対する処理の増加傾向(例: O(1), O(n), O(n^2))を示し、少ない方が効率的で、{空間計算量}(メモリ使用量)とトレードオフの関係にあることが多いです。
基本
- 目的: コンピュータの性能や外部要因に左右されず、アルゴリズム自体の効率を評価するため。
- 評価方法: 処理のステップ数(四則演算、比較、繰り返しなど)を数え、入力サイズnの関数で表現する。
- 表記: {Big-O記法}(オーダー記法)で表す。
- O(1) (定数時間): 入力サイズによらず一定時間。
- O(log n) (対数時間): 入力が増えてもゆっくり増加。※多くの場合O(log2n)を指します。
- O(n) (線形時間): 入力に比例して増加。
- O(n^2) (二乗時間): 入力nの2乗に比例して増加。
具体例
- O(n)の例: リストの全要素を1つずつチェックする処理。
- O(n^2)の例: 2つのリストを比較して重複を探す、二重ループ処理など。
補足
左から順に良い(処理時間の増加が少ない)
(良い)O(1) O(logn) O(n) O(nlogn) O(nc) (悪い)
探索アルゴリズム
探索アルゴリズムとは、膨大なデータの中から目的のデータや最適な解を見つけ出すための体系的な手順のことで、線形探索や二分探索、ハッシュ探索などが代表的です。単純に片っ端から探す方法から、データの構造や知識を利用して効率化を図る方法まで様々あり、コンピュータサイエンスの基本であり、Google検索など身近な場面でも利用されています。
| アルゴリズム | 手順の概要 | 時間計算量 |
|---|---|---|
| 線形探索 | 配列やリストなどのデータの中から、目的のデータを先頭から1つずつ順番に比較して見つける、最も単純で基本的な探索アルゴリズムです。 | O(n) |
| 二分探索 | ソート(整列)済みのデータの中から目的の値を高速に探し出すアルゴリズムで、探索範囲を中央(中間)で半分に絞り込みながら繰り返す方法です。 | O(logn) |
| ハッシュ法 | ハッシュ関数という計算式を使ってデータの格納位置(アドレス)を直接計算で求め、高速にデータを検索・管理する手法です。 | O(1) |
線形探索
線形探索(リニアサーチ、逐次探索)とは、配列やリストなどのデータの中から、目的のデータを先頭(最初)から1つずつ順番に比較して見つける、最も単純で基本的な探索アルゴリズムです。データが整列(ソート)されていなくても利用でき、見つかればそこで終了、最後まで見つからなければ存在しないと判断します。コードが単純で実装が容易ですが、データ量が多いと時間がかかるという特徴があります。

画像参照:https://www.momoyama-usagi.com/entry/info-algo-search
仕組み
- 先頭から比較: 探索対象のデータ列の先頭の要素と、探したいデータ(探索値)を比較します。
- 一致するか確認: 一致すれば探索成功、一致しなければ次の要素へ進みます。
- 繰り返す: この比較をデータ列の末尾まで繰り返します。
- 終了条件: 目的のデータが見つかった時点で終了、またはデータ列の最後まで調べても見つからなかった時点で終了します。
メリット
- 単純: 最も単純なアルゴリズムで、短いコードで実装でき、理解しやすい。
- 前処理不要: データをソート(並べ替え)するなどの前処理が不要。
- 汎用性: データが整列されていなくても使える。
- メモリ効率: 探索対象データ以外に余分な記憶領域をほとんど使わない。
デメリット
- 低速: データ量Nに対して平均でN/2回、最悪でN回の比較が必要になり、データ量が増えると時間がかかる。
- 性能: 高度なアルゴリズム(二分探索など)と比べると効率が悪い場合が多い。
応用
- リスト内の最大値や最小値を探索する際にも応用できます。
線形探索は、シンプルさと汎用性から、プログラミング学習の基本や、データ量が少ない場合、またはデータが整列されていない場合の探索で広く利用されます。
二分探索
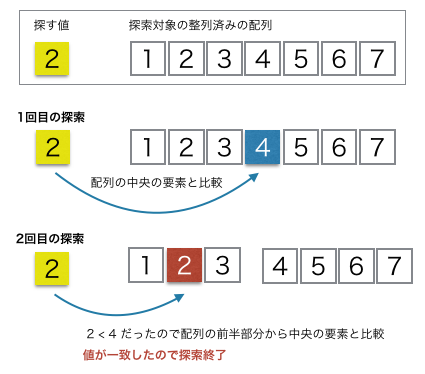
二分探索(バイナリサーチ)とは、ソート(整列)済みのデータの中から目的の値を高速に探し出すアルゴリズムで、探索範囲を中央(中間)で半分に絞り込みながら繰り返す方法です。辞書を引くように、中央の値と目的値を比較し、大きいか小さいかで「左半分」か「右半分」かを判断し、不要な部分を次々に除外します。線形探索(先頭から順に探す)に比べ、データ量が増えても必要な比較回数が対数的にしか増えない(O(log n))ため、大規模データで非常に効率的です。
画像参照:https://www.codereading.com/algo_and_ds/algo/binary_search.html
仕組み
- 前提: データが昇順(小さい順)または降順(大きい順)に並んでいる必要があります。
- 開始: 探索範囲をデータ全体の先頭から末尾までとします。
- 中央を比較: 探索範囲の中央の要素と、探したい目的の値を比較します。
- 範囲を絞る:
- 一致: 見つかったら終了。
- 目的値が小さい: 探索範囲を中央より左側(小さい方)に絞る。
- 目的値が大きい: 探索範囲を中央より右側(大きい方)に絞る。
- 繰り返し: 範囲がなくなるか、見つかるまでステップ3と4を繰り返します。
特徴
- 高速性: 線形探索の最大比較回数がn回なのに対し、二分探索は最大で
𝑙𝑜𝑔2𝑛回程度で済みます(例: 1000個のデータなら約10回)。
- 前提条件: データが事前にソート(整列)されている必要があります。未整列の場合は、ソートのコストも考慮する必要があります。
- 応用: データベースのインデックス検索、ゲームAI、辞書検索など、大量データを扱う多くの場面で利用されます。
- 関連技術: 二分探索木(Binary Search Tree, BST)のようなデータ構造の基礎にもなっています。
ハッシュ法
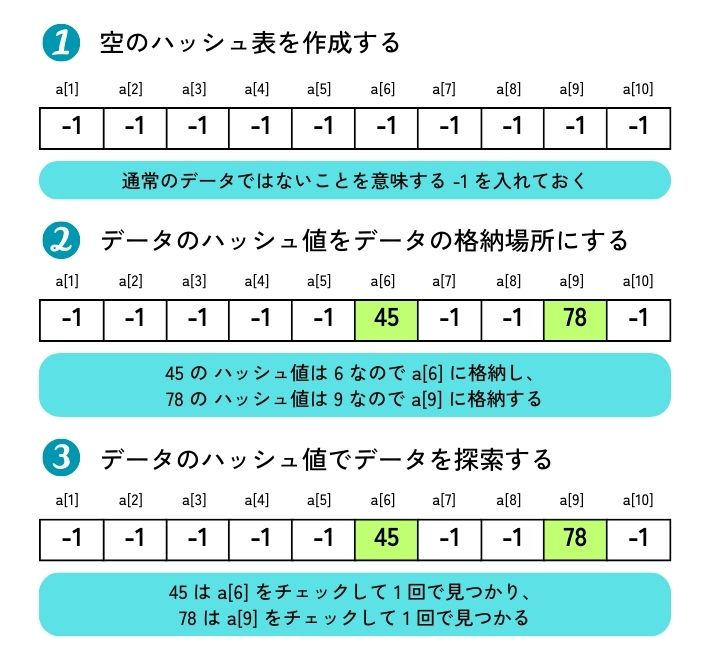
ハッシュ法とは、ハッシュ関数という計算式を使ってデータの格納位置(アドレス)を直接計算で求め、高速にデータを検索・管理する手法です。データを配列などの「ハッシュ表」に格納し、検索時には同じ計算式でアドレスを特定するため、データの増減に関わらずほぼ一定時間(O(1))でアクセスできるのが特徴で、辞書データやプログラミング言語の連想配列などで広く利用されています。
画像参照:https://www.seplus.jp/dokushuzemi/ec/fe/fenavi/similar_programming/hash_table/
仕組み
- ハッシュ関数:データを数値(ハッシュ値)に変換する計算式(例: キー値をある数で割った余り)。
- ハッシュ表(バケット):ハッシュ値に対応する格納場所(配列のインデックス)。
- 格納:キー値からハッシュ関数でハッシュ値(アドレス)を計算し、そのアドレスの場所にデータを格納する。
- 検索:検索したいデータも同じハッシュ関数でハッシュ値を計算し、そのアドレスに直接アクセスしてデータを探す。
衝突(コリジョン)と対処法
- 衝突:異なるデータが同じハッシュ値(アドレス)になる現象。
- 対処法:
- 連鎖法(チェイン法):同じアドレスのデータをリスト(鎖)でつなげて管理する。
- オープンアドレス法:空いている別の場所を探して格納する(例: 次の空きアドレスへ移動)。
具体例
- 電話番号の末尾2桁をアドレスとして、100個のイス(ハッシュ表)に座るイメージ。
- Pythonの辞書型(
dict)やRubyのハッシュなど、多くのプログラミング言語で高速なデータ管理に利用されている。


コメント