アルゴリズムは問題を解決するための手順や方法論(料理のレシピ)、データ構造はデータを効率的に整理・格納する形式(食材の保管方法)を指し、これらはプログラミングの基礎であり、適切な組み合わせでプログラムの性能(速度や効率)を大幅に向上させるために不可欠です。データ構造(配列、リスト、木など)は「何を(データ)」、アルゴリズム(探索、ソートなど)は「どうする(手順)」を決め、両者は密接に連携し、効率的なソフトウェア開発と問題解決の鍵となります。

画像参照:https://mo-gu-mo-gu.com/about-datastructure-algorithm/
木構造(ツリー構造)
木構造(ツリー構造)とは、階層的にデータが枝分かれして整理されたデータ構造で、最上位の「ルート(根)」から下位の「子」へとつながり、末端の「リーフ(葉)」まで伸びていく様子が木のようだ(逆さまにした木)と名付けられました。会社組織図、ファイルシステムのフォルダ構造、XMLデータ、DOMツリーなどで使われ、データの整理や検索を効率的に行うために利用されます。
主な特徴と用語
- 階層性: 親ノードが複数の子ノードを持ち、子ノードはさらに子を持つことで階層が深まります。
- ノード(節): ツリーを構成する各データ要素(点)。
- ルート(根): 最上位のノードで、親を持たない唯一のノード。
- リーフ(葉): 末端にあり、子を持たないノード。
- 親子関係: ルートに近いノードが親、遠いノードが子。
- エッジ(枝): ノード同士をつなぐ線。
主な用途例
- ファイルシステム: PCのフォルダ(ディレクトリ)構造。
- データベース: 階層データベース、インデックス構造。
- XML/HTML: 文書の構造表現(DOMツリー)。
- 組織図: 企業の部門・役職の階層構造。
- プログラミング: 構文解析、決定木、ソートアルゴリズム(ヒープソートなど)。
なぜツリー構造を使うのか
- データの整理: 複雑なデータを論理的な階層で分かりやすく表現できる。
- 効率的な検索: 階層構造を利用して、目的のデータを素早く見つけられる。
これらの特徴から、ツリー構造はコンピュータサイエンスの基礎であり、多様なシステムで活用されている重要なデータ構造です。
木の種類
木にはいくつか種類があります。
以降で種類ごとの概要を説明します。
二分木
二分木とは、データ構造の一種で、どの親ノード(節点)も最大2つまでしか子ノードを持たない階層的な(ツリー状の)構造のことです。子ノードは「左の子」「右の子」として区別され、二分探索木のように「左の子 < 親 < 右の子」といったルールでデータを効率的に管理・検索するために使われ、プログラミングやアルゴリズムの基礎として重要です。
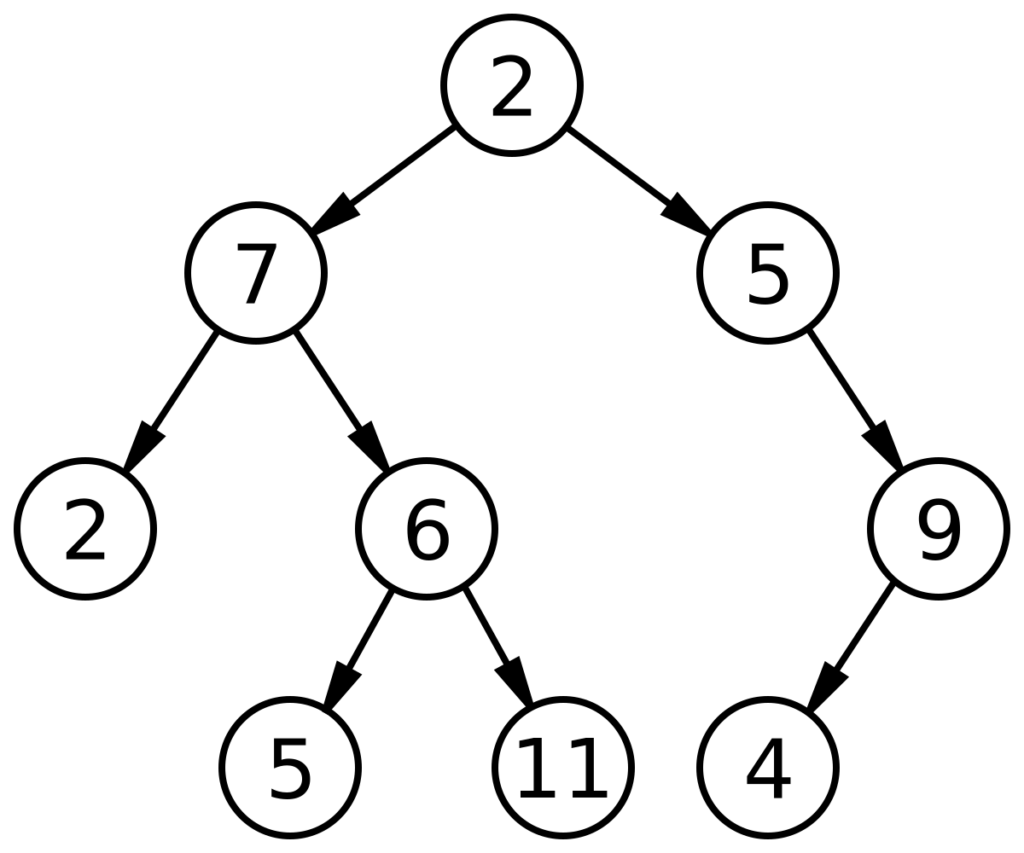
画像参照:https://ja.wikipedia.org/wiki/%E4%BA%8C%E5%88%86%E6%9C%A8
特徴
- 最大2つの子: 各ノードは子を0個(葉ノード)、1個、または2個持ちます。
- 左と右の区別: 2つの子を持つ場合、左の子と右の子は区別されます。
- 階層構造: ルート(根)から始まり、枝分かれしながら下層に広がっていく構造です。
多分木
多分木とは、データ構造(木構造)の一種で、1つの親ノード(節点)から3つ以上の子ノードに分岐できる、子の数に制限がない(またはN個まで) ことを指します。2分木が最大2つまでしか分岐しないのに対し、多分木はより柔軟な分岐が可能で、B木やB+木など、データベースなどで使われる高度な木構造の基礎となります。
特徴
- 分岐の自由度: 1つのノードから複数の(3つ以上)子ノードが伸びる。
- 2分木との対比: 2分木は子ノードが最大2つという厳しい制約があるが、多分木にはそれが無い。
- N分木: 子の数がN個(Nは3以上の自然数)に制限されたものは「N分木」とも呼ばれる。
- 表現: 結局、どんな多分木も「最初の(一番左の)子」と「兄弟ノード(右隣)」という2つの情報で表現できるため、二分木として実装することも可能。
具体例
- B木(B-tree): データベースのインデックスなどで使われ、ディスクI/Oの効率化のために設計された多分岐の木。
- デジタル木(トライ木など): 文字列検索に使われ、アルファベットの数だけ子を持つ場合(例:26分木)があり、これも広い意味での多分木。
まとめ
コンピュータサイエンスにおける「多分木」は、データの階層的な表現において、「2つまで」という制約を超えて、もっと多くの分岐(子)を持たせられる木構造全般を指す、柔軟なデータ構造の概念です。
完全二分木
完全二分木とは、すべての葉ノードが同じ深さ(レベル)にあり、かつ(葉以外の)すべての内部ノードがちょうど2つの子を持つ、隙間のない対称的な二分木のことです。また、最下層以外の階層が完全に埋まっていて、最下層は左から順にノードが詰められている木も完全二分木と呼ばれます。
代表的な完全二分木
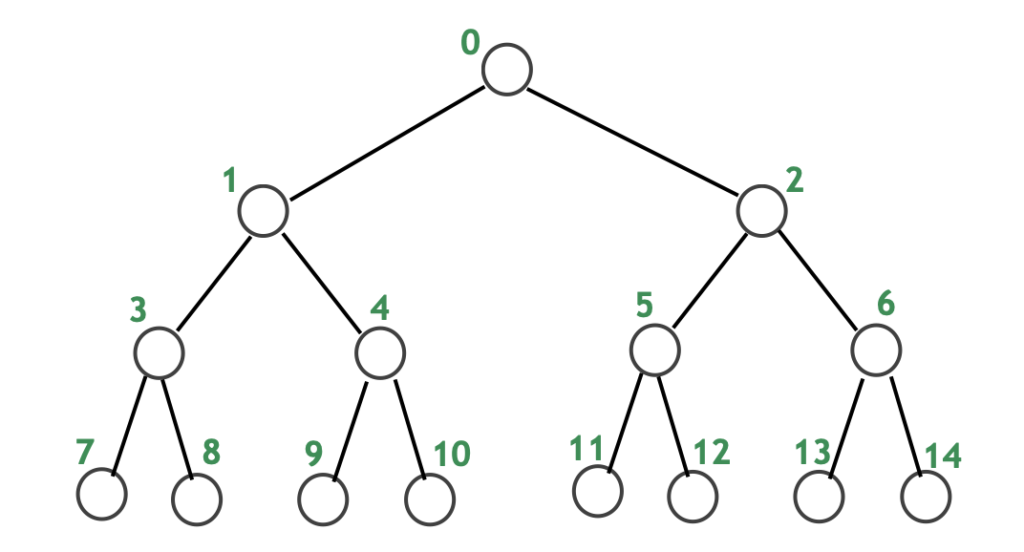
画像参照:https://algo-method.com/tasks/11587zra
補足
完全二分木の中でも、下記条件を満たすものは「ヒープ」と呼ばれます。
条件:親子間に一定の大小関係が成立していること。(例:親>子)
特徴
- すべての葉が同じ深さ: 根から最も遠い葉までの距離(深さ)がどこも同じです。
- すべての内部ノードが2つの子を持つ: 葉ではないノード(内部ノード)は必ず左と右の両方に子を持ちます。
- 隙間がない: 木の全階層がノードで満たされ、完全に対称的で「詰まった」状態です。
- 配列での実装: これらの性質から、配列(リスト)を使って効率的に表現・実装できるため、二分ヒープなどで利用されます。
二分探索木
二分探索木とは、「左の子ノードの値 < 親ノードの値 < 右の子ノードの値」という規則でデータを格納する木構造(ツリー構造)で、データの検索・挿入・削除を効率的に行うためのデータ構造です。この規則により、目的のデータを根(ルート)から探索する際に、比較するだけで探索範囲を半分に絞れるため、平均して高速()な処理が可能です。
特徴と仕組み
- 二分木であること: 各ノードは最大2つの子ノード(左の子と右の子)を持ちます。
- 値の配置ルール:
- 左の子孫は親より常に小さい値。
- 右の子孫は親より常に大きい値。
- 探索(検索):
- 根ノードから探索したい値と比較。
- 探索値が親より小さければ左へ、大きければ右へ移動。
- この操作を繰り返し、目的の値を見つけるか、葉(末端)に到達するまで続ける。
- 効率性: うまくバランスが取れていれば、
個のデータに対する探索・挿入・削除は
(対数時間)で実行されますが、データが偏ると最悪
(線形時間)になることもあります。
メリットとデメリット
- メリット:
- 高速なデータ検索・挿入・削除(平均
)。
- データをソートされた順序で取り出せる。
- 高速なデータ検索・挿入・削除(平均
- デメリット:
- データの挿入順序で木が偏ると性能が低下する(線形リストと同じになる)。
- この問題を解決するために、平衡二分探索木が使われることもあります。
主な用途
- データベースのインデックス作成
- データのソート
- 効率的なデータ管理が必要な様々なプログラミングの場面
木の巡回
木の巡回とは、木構造(ツリー構造)のすべてのノード(節点)を、特定の順序で1回ずつ訪問(処理)していくアルゴリズムのことで、データを取り出したり、処理したりする際に使われ、主に「幅優先探索」と「深さ優先探索」の先行順(行きがけ順)、中間順(通りがけ順)、後行順(帰りがけ順)があります。
幅優先探索
幅優先探索とは、グラフや木構造を探索するアルゴリズムで、始点(スタートノード)から近いノードを優先的に、波紋のように横方向へ広がりながら段階的に探索していく方法です。
具体的には、始点から距離1のノードを全て調べ、次に距離2のノードを全て調べ…と、「近い順」に探索を進めるため、最短経路の探索(カーナビの経路探索やSNSでの友達の友達をたどるイメージ)などに利用され、キューというデータ構造(先入れ先出し)を使って実装されます。
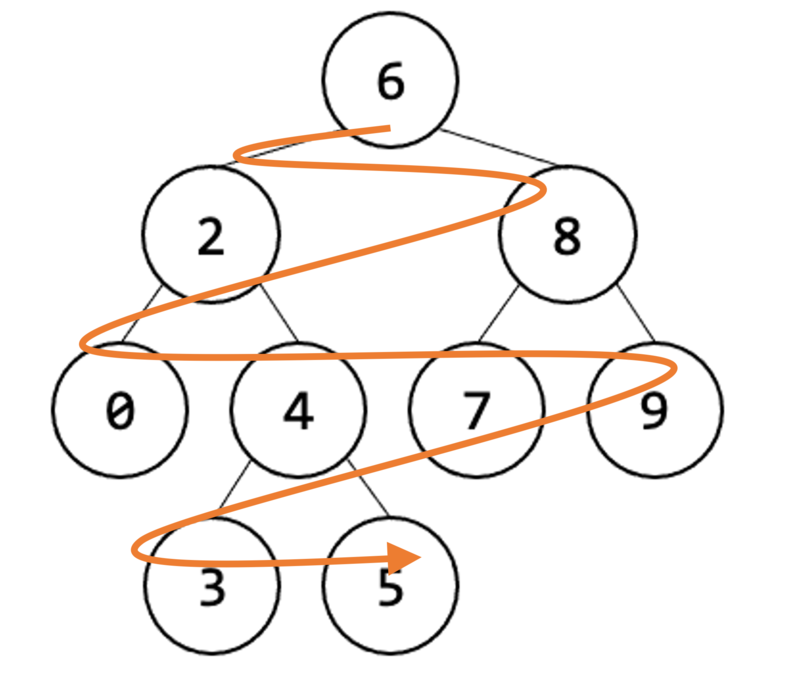
画像参照:https://inarizuuuushi.hatenablog.com/entry/2022/10/31/090000
特徴
- 探索順序: 始点からの距離が同じノードはまとめて探索され、遠いノードは後回しにされます。
- データ構造: 探索候補の管理にキュー(FIFO)を使います。
- 用途:
- 最短経路の探索(辺の重みが同じ場合)。
- ネットワークの到達可能性の確認。
- 「友達の友達」のような階層的な関係の探索。
深さ優先探索
深さ優先探索とは、グラフや木構造を探索するアルゴリズムの一種で、ある一つの経路を可能な限り深く(行き止まりまで)進み、行き詰まったら一つ戻って別の経路を探すという方法です。スタック(後入れ先出し)のデータ構造を利用するか、再帰処理を使って実装され、メモリ効率が良いという特徴があります。
仕組み
- 開始: 始点となるノード(頂点)から探索を開始します。
- 深く進む: 隣接するノードのうち、まだ訪れていないノードを一つ選び、ひたすらその方向に進んでいきます。
- 行き止まり: それ以上進めなくなったら(行き止まり)、一つ前のノードに戻ります(バックトラック)。
- 別ルート探索: 戻った場所で、まだ探索していない別の隣接ノードがあれば、そこから再び深く探索を始めます。
- 繰り返し: これを全てのノードが探索されるまで繰り返します。
種類
木構造のノードを「根(ルート)」、「左部分木」、「右部分木」として捉え、これらの訪問順序によって名前が変わります。
- 先行順(行きがけ順): 根 → 左部分木 → 右部分木。
- 中間順(通りがけ順): 左部分木 → 根 → 右部分木(二分探索木ではソートされた順に出力される)。
- 後行順(帰りがけ順): 左部分木 → 右部分木 → 根。
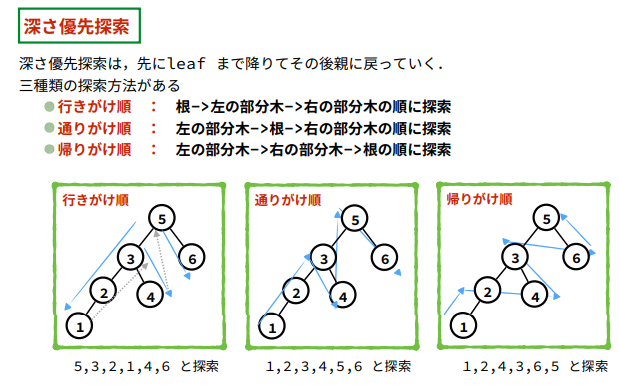
画像参照:https://qiita.com/lymansouka2017/items/6ba22c234a348df3e1b7


コメント